Four-Look Last Layer
Two-Look OLL and PLL split each of the two steps of Fridrich last layer into two, corners and edges. As this greatly reduces the number of algorithms required, these serve as perfect stepping stones before advancing to full PLL and OLL.
Two-Look OLL
These algorithms are all taken straight from my full OLL. One of three algorithms (OLL 1, 44, 45) corrects the edge orientation, and then corner orientation is corrected while preserving the edge orientation using one of seven algorithms (OLL 21-27). For edge orientation, any algorithm with the same effect on the edges can be used; 1, 44, and 45 are just particularly easy to perform.
Edge Orientation
| Codes | Pattern | Algorithm | How It's Done |
| a (1) |  |
RU2'-R2'FRF'U2'-R'FRF' | |
| b (44) |  |
FwRUR'U'F'w | |
| c (45) |  |
FRUR'U'F' |
Corner Orientation
| Codes | Pattern | Algorithm | How It's Done |
| 21 |  |
RU-R'URU'R'UR-U2'R' | |
| 22 |  |
RU2'-R2'U'R2U'R2'-U2R | |
| 23 |  |
R2DR'U2RD'R'U2'R' | |
| 24 |  |
RwUR'U'R'wFRF' | |
| 25 |  |
Lw'U'L'U-RU'LUx' | |
| 26 |  |
R'U'RU'R'U2R | |
| 27 |  |
RUR'URU2'R' |
Two-Look PLL
Corner Permutation
If the corner permutation is not solved, we can always AUF (Adjust U Face) to correctly place exactly two corners. We therefore only have two distinct cases: adjacent swap and diagonal swap. If there are two adjacent corners sharing the same color on the same side, we are in the adjacent swap case. Bring these to the back and rotate the bottom two layers until the UFL corner is matched. We recognize this as a 3-cycle:
| Codes | Pattern | Algorithm | How It's Done |
| n4 Acw |
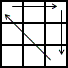 |
xR'UR'DDRU'R'DDR2x' |
We never need the other direction.
If the corners do not share a color on any side, we are in the diagonal swap case. You can use any of the several diagonal-swap PLL algorithms. I recommend the Y-perm:
| Codes | Pattern | Algorithm | How It's Done |
| n15 Y |
 |
FRU'R'U'RUR'F'-RUR'U'R'FRF' |
Edge Permutation
With the corners matched, there are only four possible edge permutation cases.
| Codes | Pattern | Algorithm | How It's Done |
| n1a U |
 |
R'UR'U'-R'U'-R'URUR2 | |
| n2a U |
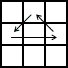 |
R2U'R'U'RURURU'R | |
| n5 Z |
 |
UR'U'RU'RURU'R'URUR2U'R'U | |
| n6 H |
 |
M2'UM2'U2M2'UM2' |